5187. Точка пересечения высот

Найдите точку пересечения высот данного треугольника.

Вход. Координаты трех вершин треугольника (сначала координаты первой вершины, затем второй, затем третьей). Координаты – пара целых чисел, не превосходящих 10⁴ по модулю.

Выход. Выведите два числа – координаты точки пересечения высот данного треугольника с точностью не меньше 6 десятичных знаков.

Пример входа	Пример выхода
0 0 3 0 0 4	0.0 0.0

РЕШЕНИЕ

геометрия

Анализ алгоритма

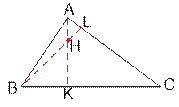
Пусть A(x_a, y_a), B(x_b, y_b), C(x_c, y_c) – три вершины треугольника. Проведем высоты AK и BL. Точка их пересечения H будет искомой.

Напишем уравнение прямой AK: она должна проходить через вершину A и быть перпендикулярной прямой BC. Пусть уравнение прямой AK имеет вид a₁x + b₁y = c₁. Тогда вектор (a₁, b₁) совпадает с направлением вектора BC и можно положить (a₁, b₁) = (x_c – x_b, y_c – y_b). Уравнение прямой AK примет вид

(x_c – x_b)x + (y_c – y_b)y = c₁

Поскольку прямая AK проходит через точку А, то подставив в ее уравнение координаты точки A(x_a, y_a), найдем значение c₁:

(x_c – x_b) x_a + (y_c – y_b) y_a = c₁

Аналогично находим уравнение прямой BL. Пусть оно имеет вид a₂x + b₂y = c₂. Вектор (a₂, b₂) совпадает с направлением вектора АC и можно положить (a₂, b₂) = (x_c – x_a, y_c – y_a). Точка B лежит на прямой BL, следовательно

(x_c – x_a) x_b + (y_c – y_a) y_b = c₂

Точка пересечения высот треугольника находится решением системы уравнений

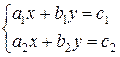
методом Крамера.

Реализация алгоритма

Функция kramer находит решение (x, y) системы уравнений

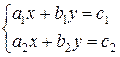
void kramer(double a1, double b1, double c1,

double a2, double b2, double c2, double &x, double &y)

{

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

x = dx / d; y = dy / d;

}

Читаем входные данные.

scanf("%lf %lf %lf %lf %lf %lf",&xa,&ya,&xb,&yb,&xc,&yc);

Находим уравнение прямой AK: a₁x + b₁y = c₁.

a1 = xc - xb;

b1 = yc - yb;

c1 = xa * (xc - xb) + ya * (yc - yb);

Находим уравнение прямой BL: a₂x + b₂y = c₂.

a2 = xc - xa;

b2 = yc - ya;

c2 = xb * (xc - xa) + yb * (yc - ya);

Находим и выводим точку пересечения высот треугольника.

kramer(a1,b1,c1,a2,b2,c2,x,y);

printf("%.6lf %.6lf\n",x,y);

Java реализация

import java.util.*;

public class Main

{

static double[] kramer(double a1, double b1, double c1,

double a2, double b2, double c2)

{

double res[] = new double[2]; // x, y

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

res[0] = dx / d;

res[1] = dy / d;

return res;

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

double xa = con.nextDouble();

double ya = con.nextDouble();

double xb = con.nextDouble();

double yb = con.nextDouble();

double xc = con.nextDouble();

double yc = con.nextDouble();

double a1 = xc - xb;

double b1 = yc - yb;

double c1 = xa * (xc - xb) + ya * (yc - yb);

double a2 = xc - xa;

double b2 = yc - ya;

double c2 = xb * (xc - xa) + yb * (yc - ya);

double res[] = kramer(a1,b1,c1,a2,b2,c2);

System.out.println(res[0] + " " + res[1]);

con.close();

}

}